Финансовая математика

Решение:

Представим данную сделку как поток наличности:

прибыль вексель доходность сделка

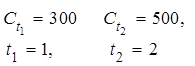
Найдём текущую стоимость на момент времени t = 0 для дискретного потока наличности по формуле:

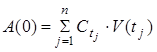
где - дисконтирующий множитель.

Получим:

А(0) = 300 ∙ е 0,02 + 500 ∙ е 0,02 ∙ 2 = 300 ∙ 1,0202 + 500 ∙ 1,0408 = 826,5

Разделим эту сумму на 3 квартала, получим размер регулярного платежа: 826,5 : 3 = 275,5 у.д.е.

Задача 51

Заданы сделки в виде дискретных потоков наличности, определённых таблицами:

где - доходы или расходы, выраженные в условных денежных единицах; соответственно tj - моменты времени, в которые происходят поступления или выплаты денег. Требуется: а) составить уравнение стоимости; б) определить, имеет ли сделка доходность; в) решить уравнение стоимости, если сделка имеет доходность, и вычислить с точностью до одного процента.

Решение:

а) Уравнение стоимости для данной сделки имеет вид:

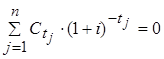
Или: -5(1 + i) -1 + 3(1 + i) -3 - 2(1 + i) -4 + 9(1 + i) -6 = 0

Упростим данное уравнение, умножив обе его части на множитель (1 + i)6. Получим: - 5(1 + i)5 + 3(1 + i)3 - 2(1 + i)2 + 9 = 0

б) По правилу 1 вычислим итоговые суммы:

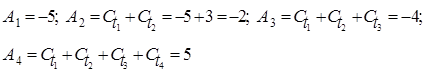
Таким образом, последовательность

имеет одну перемену знака (вначале следуют отрицательные члены, затем положительные), причём . Сделка имеет доходность.

в) Для нахождения доходности воспользуемся методом бисекции или деления отрезка пополам. Введём функцию:

f(i) = -5(1 + i)5 + 3(1 + i)3 - 2(1 + i)2 + 9 = 0

Решение уравнения будем искать при . Найдём вначале интервал, на концах которого функция принимает значение противоположных знаков. Тогда, как известно, корень находится внутри найденного интервала. Такой интервал находится подбором: